(βx)^n / (exp(αx) - 1) の広義積分

まず，結果を示します. 変数の係数は全て正としています. 

ここで，右辺の特殊関数はそれぞれ，ガンマ関数およびゼータ関数で

と表されます. 

それでは過程へ入ります. 

------------------------------------------------------------------------

まず，被積分関数について，前回の記事と同じ様に等比級数の和を用いると，

と書くことができ，更に，この数列は収束するので項別積分ができて，結局は

となります. ここで，総和記号内の積分に於いては，一旦文字で置き，

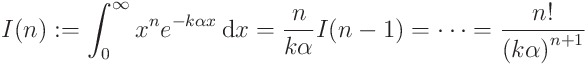
となるので，再び与式を書き改めてみると，

となるので，最初に述べたガンマ関数及びゼータ関数を用いれば，結果の

となります. ■

--------------------------------------------------------------------------

試しに値を代入してみると，

となりました. ここで，

を用いました.